Spin-canting-induced band reconstruction in the Dirac material
Ca1-xNaxMnBi2
The ternary AMnBi2 (A= alkaline as well as rare-earth atom) materials provide an arena for investigating the interplay between low-dimensional magnetism of the antiferromagnetic MnBi layers and the electronic states in the intercalated Bi layers, which harbour relativistic fermions. In our first attempt (see Fermi surface instability in topological materials) to study the link between the anomaly in the dc resistivity with onset at Ts and the electronic properties of the title compound, we uncovered optical signatures for a partial gapping of the Fermi surface (FS), for energy scales up to 0.2 eV. This may reveal the inclination towards a FS instability in topological materials, accompanied by a sizeable depletion of the density-of-states (DOS) at the Fermi level (EF).
The present work intends to precisely address the microscopic origin of the FS gapping. To this end, we study Ca1-xNaxMnBi2 at three dopings (x = 0, 0.03 and 0.05) and as a function of temperature (T) with magnetic torque measurements, as well as with the support of first-principles calculations. Our findings give evidence for a spin-canting occurring at Ts ~50–100 K (Fig. 1.14).
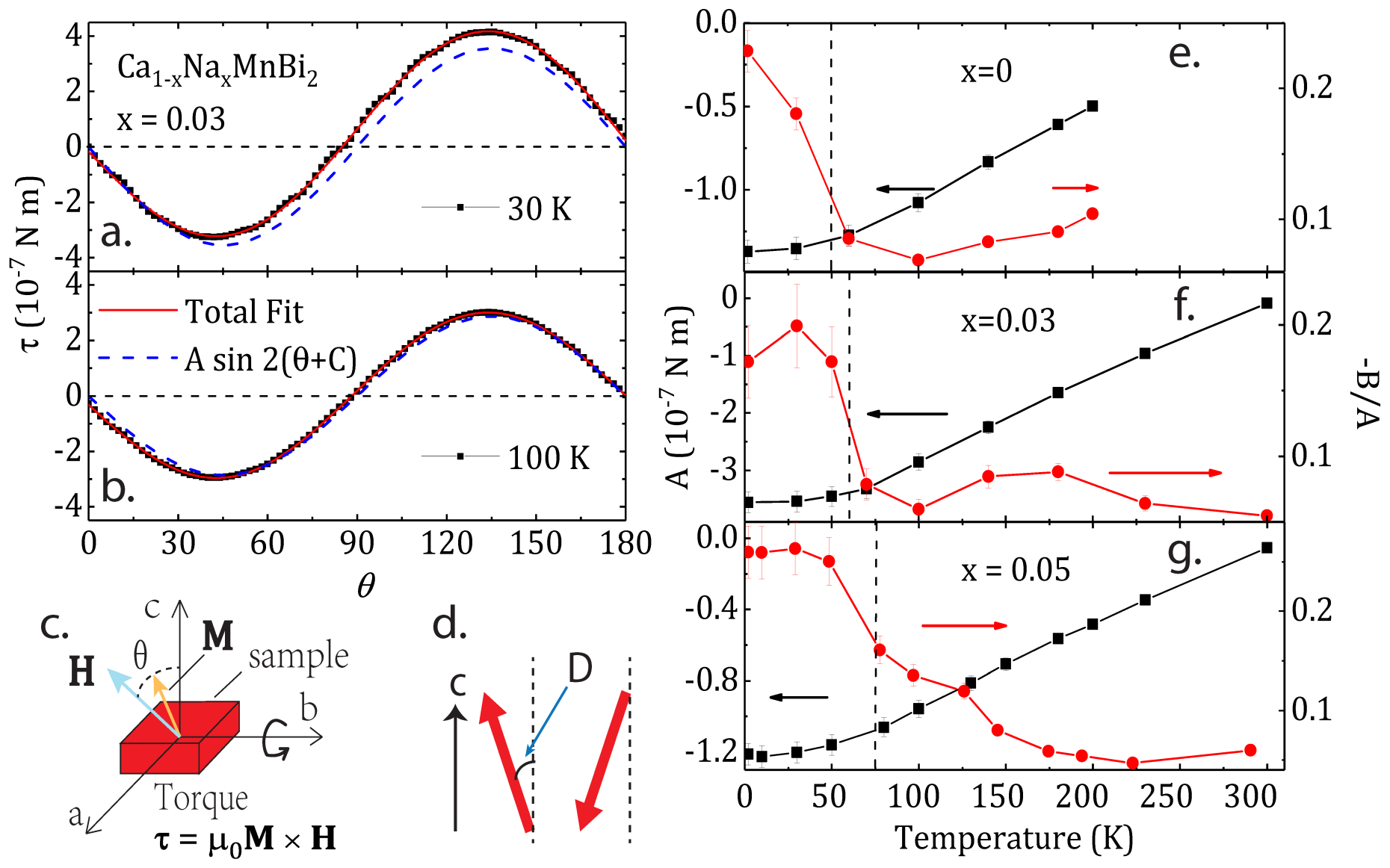
Our first-principles calculations establish that the spin-canting leads to the reconstruction of the electronic band structure, having immediate implications for the spectral weight reshuffling in the optical response (i.e., partial gapping of FS) and the dc transport properties below Ts (Fig. 1.15). Obviously, if spin-canting is the principle driving mechanism for the reconstruction of the electronic band structure below Ts, as revealed by our experiments, we might expect the realisation of Weyl states in Na-doped CaMnBi2, as a consequence of the broken time-reversal symmetry. This is of wider interest, because of the peculiar Dirac band crossing along a continuous line in momentum space in CaMnBi2.
