Charge dynamics of the Co-doped BaAs2Fe2
A new field in condensed matter research was recently initiated by the discovery of superconductivity in doped iron oxyarsenides. While the nature of superconductivity is currently in dispute, it was soon evident that it emerges from specific structural and electronic conditions in the FeAs layer. The recently discovered BaAs2Fe2 compound is another excellent oxygen-free candidate. Superconductivity was indeed established at 38 K in K-doped and at 22 K in Co-doped BaAs2Fe2 through partial substitution of the Ba and Fe site, respectively. Superconductivity in suitably doped BaAs2Fe2 compounds conclusively proves that it originates only from the iron arsenide layers, regardless of the separating sheets. It is also currently believed that the superconductivity in these systems is intimately connected with magnetic fluctuations and a spin-density-wave (SDW) anomaly within the FeAs layers. This is obviously of interest, since a SDW phase may generally compete with other possible orderings and complicated phase diagrams are often drawn due to their interplay.
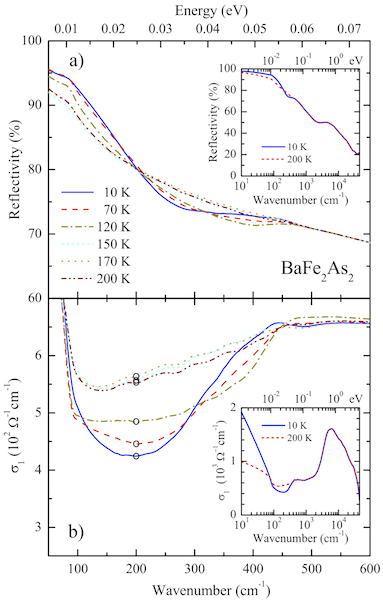
We first focused our attention on BaAs2Fe2, providing a thorough investigation of the optical response over an extremely broad spectral range at temperatures both above and below TSDW. Panel a) of Fig. 2.10 displays the optical reflectivity in the FIR energy interval, emphasizing its temperature dependence. The inset of panel a) in Fig. 2.10 shows on the other hand the reflectivity R(ω) over the whole measured range at 10 and 200 K. Of interest is the temperature dependence of R(ω), which first indicates a depletion of R(ω) with decreasing temperature in the energy interval between 200 and 500 cm-1 and then a progressive enhancement of R(ω) below 200 cm-1 and towards zero frequency, so that all R(ω) spectra cross around 200 cm-1. Panel b) of Fig. 2.10 then shows the real part σ1(ω) of the optical conductivity at various temperatures, resulting from the KK transformation of the measured R(ω). In its inset we display the overall optical conductivity at 10 and 200 K. From the data as well as from their phenomenological Lorentz-Drude analysis emerges a picture in which at T > TSDW delocalized states (i.e. free charge carriers close to the Fermi level), represented by the Drude term, coexist with more localized or low-mobility states, described in σ1(ω) by three FIR Lorentz h.o.'s. When lowering the temperature below TSDW, a pseudogap develops and a rearrangement of states takes place in such a way that excitations pile up in the spectral range around 420 cm-1 as well as around 50 cm-1. These latter excitations merge into the high frequency tail of the narrow Drude term of σ1(ω). Such a redistribution of spectral weight governs the appearance of the depletion in σ1(ω) between 100 and 400 cm-1 below TSDW.

Following a well established procedure, we extract the characteristic average weighted energy ωSP, which is ascribed to the representative energy scale for the pseudogap excitation, resulting below TSDW from the reshuffle of states at energies lower than the mobility edge. ωSP is shown in Fig. 2.11, normalized by its value at 10 K. The increase of ωSP goes hand in hand with the decrease of σ1(ω) in the energy interval around 200 cm-1. We also calculate the quantity λ= σ1(200 cm-1,T)/σ1(200 cm-1,10 K), and find indeed that λ-1 scales with ωSP as a function of temperature (Fig.2.11). As far as the Drude term is concerned, its narrowing is well represented by the decrease of the Drude scattering rate ΓD parameter with decreasing temperature. The inset of Fig. 2.11 displays the scattering rate from our Lorentz-Drude fit as a function of temperature together with dc resistivity data taken for samples prepared by the same technique. Both quantities are normalized to their respective values at 200 K and follow the same trend in temperature above as well as below TSDW. The SDW transition reduces the possible scattering channels so that the resistivity and the Drude scattering rate decrease rather abruptly below TSDW.
Our strategy recently consisted in comparing the electrodynamic response of Ba(Fe1-xCox)2As2 for several Co-dopings, which belong to the so-called 122 family and are prominent examples of oxygen-free iron-pnictide superconductors. We presented systematic measurements across the phase diagram, from underdoped non-superconducting (x = 0 and 0.025), to underdoped superconducting (x = 0.051), to near optimal doping (x = 0.061), to overdoped superconducting (x = 0.11) and finally to overdoped non-superconducting (x = 0.18) compositions. Particular emphasis was devoted to the impact of the various transitions on the charge dynamics in these Co-doped 122 materials. Our primary goal was to exploit their electrodynamic response in order to establish with spectral weight argument their degree of electronic correlations.
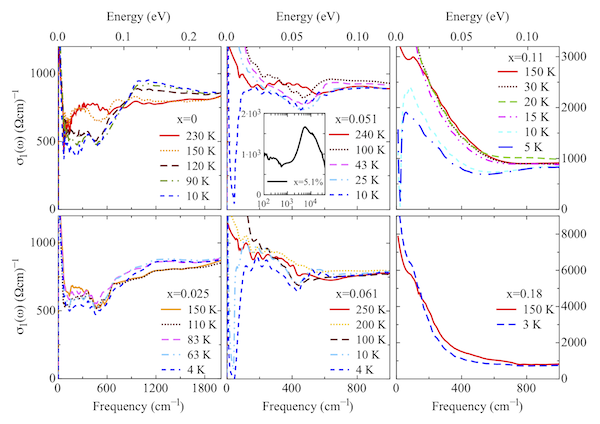
Figure 2.12 highlights the temperature dependence of σ1(ω) for all dopings in the energy ranges pertinent to the SDW and superconducting transition. The excitation spectrum at high frequencies, shown in the inset of Fig. 2.12, is identical for all Co-dopings and is consistent with previous investigations. There is a strong absorption band peaked at about 5000 cm-1, further characterized by a broad high frequency tail and generally ascribed to the contribution due to the electronic interband transitions. σ1(ω) for x = 0 suddenly decreases below 800 cm-1 at temperatures below TSDW. This leads to a depletion in the range between 200 and 800 cm-1, inducing a removal of spectral weight. The depletion as well as the peak at about 800 cm-1 in σ1(ω) are indicative for the opening of a pseudogap, which we identify with the SDW single particle excitation (see above for further details). For x = 0.025 Co-doping, the depletion as well as the (pseudo)gap feature in σ1(ω) are less evident and pronounced, even though there is a spectral weight redistribution, leading again to its overshoot above 700 cm-1 for temperatures below TSDW. The signatures for the SDW pseudogap-like excitation as well as the related spectral weight redistribution are no longer well distinct for the x = 0.051 Co-doping. For this latter compound as well as at and above the optimal Co-doping (x = 0.061 and 0.11, respectively), the total reflection at ω < ωg for T << Tc leads instead to the opening of the superconducting gap. The removed spectral weight is shifted into the collective excitation at zero frequency. Finally, the electrodynamic response of the x = 0.18 compound merely displays a simple metallic behavior. We shed light on the spectral weight redistribution between the itinerant (coherent) and the localized (incoherent) portion of the conduction band, from where we extracted the ratio between the coherent weight and the total one up to the electronic interband transitions (i.e. including the incoherent weight, as well). Such a ratio is a measurement of the degree of electronic correlations. We argue that the 122 iron-pnictides fall in the regime of moderate electronic correlations for the parent compound and close to optimal doping, while a conventional metallic behavior in the nearly free electron limit is recovered at the opposite, overdoped, end of the superconducting dome in their phase diagram.