Magneto-optical reflectivity of superconducting MgB2 single crystals
Since the discovery of superconductivity in MgB2 with Tc ~40 K, substantial experimental activity has been devoted to elucidate the nature of its superconducting state. The issue is to assess whether MgB2 is one of the best-optimized Bardeen-Cooper-Schrieffer (BCS) materials or whether its superconducting properties stem from a novel pairing mechanism. The amplitude of the superconducting gap and its spectroscopic signature, as a function of temperature and magnetic field, are expected to depend on the driving mechanism.
Infrared spectroscopy is a very promising and powerful method for the observation of the gap. Optical experiments, besides being contact-less techniques, offer the important advantage that the electromagnetic radiation penetrates deeply inside the bulk. We have presented infrared reflectivity data R(ω) on high quality single crystals of MgB2 with well-characterized optical surface parallel to the basal-plane. The data were collected as a function of temperature (1.5-300 K) and with varying magnetic field H (0-7 T) oriented along the c-axis with possible misalignment of less than 5º.
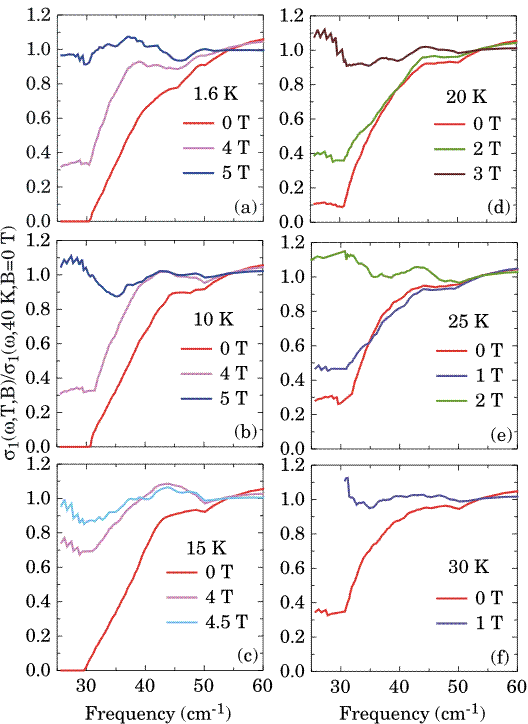
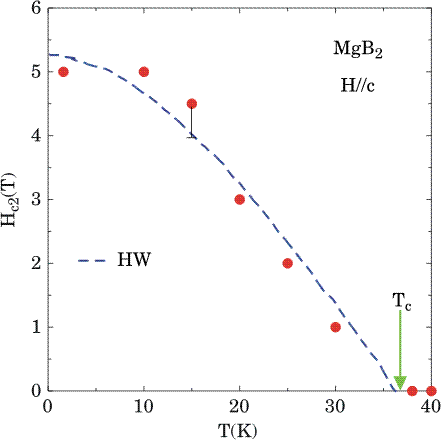
The corresponding real part of the optical conductivity exhibits a depletion of oscillator strength due to the opening of the superconducting gap (Fig. 2.6) The gap size is less than half the value expected from an isotropic BCS model. By applying magnetic fields along the c-axis we induce a suppression of superconductivity, as suggested by the disappearance of the gap. We extract the upper critical field Hc2 along the c-axis (Fig. 2.7) and find it to be compatible with the Helfand-Werthamer calculation. This seems to indicate that no unconventional mechanism needs to be invoked to explain the bulk upper critical field. Moreover, our magneto-optical results suggest a dirty-limit metallic normal state.